Number Systems

December 10, 2022
Read Time: 4 mins 38 secs
Word Count: 1103

A number system defines a set of values used to represent quantity. The number system in most common use today is the Arabic system. It was first developed by the Hindus and was used as early as the 3rd century BC. The introduction of the symbol "0," used to indicate the positional value of digits, was very important. We thus became familiar with the concept of groups of units, tens of units, hundreds of units, thousands of units, and so on. In number systems, it is often helpful to think of recurring sets, where a set of values is repeated over and over again.

Considering the decimal number system, it has a set of values, that range from 0 to 9. This basic set is repeated over and over, creating large numbers. Each increase in value occurs, till the value of the largest number in the set is reached (9), at which stage the next value is the smallest in the set (0) and a new value is generated in the left column (i.e., the next value after 9 is 10). Example: 09, 10—19, 20—29, 30—39, etc.

We always write the digit with the largest value on the left of the number. This concept is applicable to all number systems. The base value of a number system is the number of different values the set has before repeating itself. For example, decimal has a base of ten values, 0 to 9.

• Binary = 2 (0, 1)
• Octal = 8 (0 - 7)
• Decimal = 10 (0 - 9)
• Duodecimal = 12 (used for some purposes by the Romans)
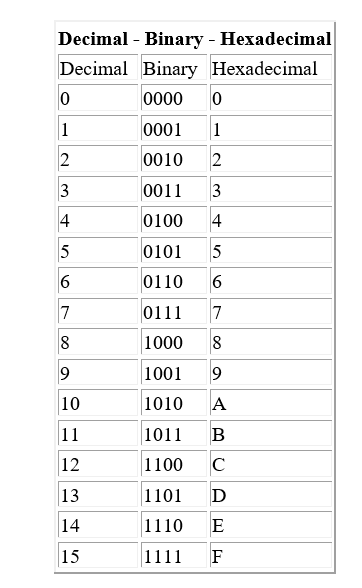
• Hexadecimal = 16 (0 - 9, A-F)
• Vigesimal = 20 (used by the Mayans)
• Sexagesimal = 60 (used by the Babylonians)

The weighting factor is the multiplier value applied to each column position of the number. Decimal, for example, has a weighting factor of TEN, which means that each column to the left represents a multiplication value increase of 10 over the previous column to the right, i.e., each column move to the left increases in a multiply factor of 10.Example: 312 = (2 * 100) + (1 * 101) + (3 * 102).

Binary Number System [Base-2]

The binary number system uses TWO values to represent numbers. The values are 0 and 1, with 0 having the least value, and 1 having the greatest value. Columns are used in the same way as in the decimal system, in that the left most column is used to represent the greatest value. In a computer, a binary variable capable of storing a binary value (0 or 1) is called a BIT. The binary number system is also a positional numbering system. Each binary digit has its own positional value or weight expressed as a power of 2. For a binary number, the binary point separated the whole number part from the fractional part. The place values of the digits to the right of the binary point are obtained by raising 2 to successive negative powers. In this binary system, there are only two values (0 - 1) in the set, so columns represent multiplication values of 2.

Example: 1011 = (1 * 20) + (1 * 21) + (0 * 22) + (1 * 23) = 11 (in decimal).

Octal Number System [Base-8]

The octal number system uses EIGHT values to represent numbers. The values are 0 (1, 2, 3, 4, 5, 6, and 7), with 0 being the lowest and 7 being the highest.Columns are used in the same way as in the decimal system, in that the left-most column is used to represent the greatest value. The octal number system is also a positional numbering system. Each octal digit has its own positional value or weight expressed as a power of 8.

Decimal Number System [Base-10]

This number system uses TEN different symbols to represent values. The set values used in decimal are: 0 1 2 3 4 5 6 7 8 9, with 0 having the least value and nine having the greatest value. The digit or column on the left has the greatest value, while the digit on the right has the least value. When doing a calculation, if the highest digit (9) is exceeded, a carry occurs, which is transferred to the next column (to the left).

Hexadecimal Number System [Base-16]

The hexadecimal number system uses SIXTEEN values to represent numbers. The values are 0 1 2 3 4 5 6 7 8 9 A B C D E F, with 0 having the least value and F having the greatest value. Columns are used in the same way as in the decimal system, in that the left most column is used to represent the greatest value. In computer systems, hexadecimal is frequently used to represent values [numbers and memory addresses].

Converting Decimal to Binary

There is a number of ways to convert between decimal and binary.

Method 1: Divide the number by 2, and then divide what's left by 2, and so on until there is nothing left (0). Write down the remainder (which is either 0 or 1) at each division stage. Once there are no more divisions, list the remainder values in reverse order. This is the binary equivalent.

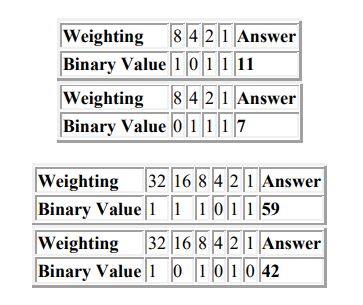
Method 2: Each column represents a power of 2, so use this as a basis of calculating the number. It is sometimes referred to as the 8:4:2:1 approach. Write down the binary number. Where a 1 appears in the column, add the column value as a power of 2 to a total.

CONVERTING DECIMAL TO BINARY

Problem: Convert 176 in octal to decimal.

Each column represents a power of 8.

176 = (6 * 80 ) + (7 * 81 ) + (1 * 82 ) = 126

Octal was used extensively in early mainframe computer systems.

Converting hexadecimal to decimal

Problem: Convert 176 in hexadecimal to decimal.

Each column represents a power of 16.

176 = (6 * 160 ) + (7 * 161 ) + (1 * 162 )
= 6 + 112 + 256
= 374

Converting binary to hexadecimal

Problem: Convert 10110 to hexadecimal.

Each hexadecimal digit represents 4 binary bits.
Split the binary number into groups of 4 bits, starting from the right.

[1] [0110] = 1 6 = 16 in hexadecimal

Converting decimal to hexadecimal

Problem: Convert 232 decimal to hexadecimal.

Use the same method used earlier to divide decimal to binary, but divide by 16.
= E816